The Chemical Bond: Sigma (σ) Bonds

Sigma bonds

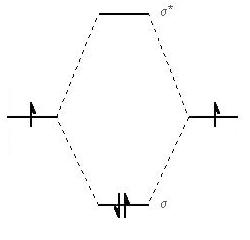
The simplest example of a σ bond is that formed between two hydrogen atoms.

First, let's consider what happens to the energy of two H atoms as they get closer to each other from infinite separation (see Figure 1.).

Energy (kJ/mol) H2 Bond Dissociation Reaction H - H bond distance (Å)

Figure 1. Potential Energy (PE) Curve for the Formation of H₂

The attraction of the electrons to the nuclei of the other atom stabilizes the system until they get so close that the nuclei start to repel each other. It is a balancing act between the attractive forces between nuclei and electrons, and replusions between nuclei and between electrons, see Figure 2 below.

Figure 2: Electrostatic attractive and replsuive forces in a mocleule.

The most stable (lowest energy) state corresponds to the equilibrium H-H bond length 74 pm.

The energy difference between the most stable state and the energy at infinite separation (zero by definition) corresponds to the H-H bond strength (or Bond Dissociation Energy (BDE)).

A of the formation of H₂. (Note: the animation is large, wait until the background turns white before playing.)

A of the formation of H₂, color coded by the electron density. (Again the animation is large, wait until the background turns white before playing.)

A of the formation of H₂ σ^* anti-bonding orbital. (Again the animation is large, wait until the background turns white before playing.)

The Hydrogen Molecule

The atomic orbitals of the two hydrogen atoms, the 1s orbitals, are represented on the outsides by two blue spheres.  In the middle are the in-phase and out-of-phase combinations for the molecule.  Remember, the "phase" of an orbital arises from the mathematical expression that describes the shape of the orbital. This is important in bonding since the two orbitals that will form the bond must have the same phases to overlap and produce a new bonding molecular orbital. If they are "out-of-phase" they can not overlap and share electrons. The in-phase (HA-1s + HB-1s) combination is at lower energy than the 1s orbitals we started from and is called the bonding molecular orbital since it is responsible for sharing the electron density between the two nuclei. This molecular orbital is symmetrical with respect to rotation about an axis on which both H nuclei lie, this is termed a "sigma" orbital  i.e.  σ-orbital.
The out-of-phase combination (HA-1s - HB-1s) is at higher energy than the 1s orbitals we started from. Subtracting the two 1s orbitals produces a "node" in the orbital which in this case is a plane perpendicular to the internuclear axis half way between the two H atoms. Remember a node is a point where the probability of finding the electron(s) is zero. This orbital is called the anti-bonding molecular orbital since the presence of electrons in this orbital will cause the bond to break, i.e. think of He2. With a total of four electrons both the bonding and anti-bonding orbitals would be occupied and there would be no net bonding effect between the atoms. This is the reason He2 does not exist. The anti-bonding σ-orbital is also symmetrical with respect to rotation about an axis on which both H nuclei, so it is also a σ-orbital, but because it is the out-of-phase combination it is termed a "sigma-star" orbital i.e.   σ*-orbital. The electrons are "placed" in the molecular orbitals following the same rules as for filling orbitals in atoms (i.e. lowest energy level first, spin-pairing as you go). This means the two 1s electrons both go into the bonding molecular orbital, this results in the stabilization of the system. Hence, two H atoms combine to become more stable as a H2 molecule. IMPORTANT:  Only orbitals containing electrons contribute to the stability of the molecule, so the empty σ*-orbital has no impact here.
	H atomic orbital H2 molecular orbital H atomic orbital
The σ bond can be formed by the overlap between: s orbitals (see above) i.e. any combination that produces a bonding molecular orbital with the electron density located along the internuclear axis.